Hilbert transform 希尔伯特变换

“The Hilbert transform is a way to convert a real-value-only time series to its complex representation (one that contains both a real part and an imaginary part), which in turn allows power and phase values to be extracted. The Hilbert transform involves computing a Fourier transform, rotating the positive frequencies (those between zero and the Nyquist) by -90° in complex space, rotating the negative frequencies (those above the Nyquist) by 90°, summing the rotated frequencies back onto the original frequencies, and then computing the inverse Fourier transform. In practice, this can be implemented by doubling the positive frequencies, zeroing-out the negative frequencies, and computing the inverse Fourier transform. This produces a times series of complex numbers.” (Mike X Fundamentals of Time-Frequency Analyses in Matlab/Octave, p. 96) 希尔伯特变换是一种将仅有实值的时间序列转换为其复数表示(一个同时包含实部和虚部)的方法，进而可以提取功率和相位值。希尔伯特变换涉及到计算一个傅里叶变换，在复数空间将正频率(介于零和奈奎斯特之间)旋转- 90°，将负频率(高于奈奎斯特)旋转90°，将旋转后的频率和回到原来的频率，然后计算傅里叶逆变换。在实际应用中，这可以通过将正频率加倍、负频率置零和计算傅里叶逆变换来实现。这就产生了一系列的复数。

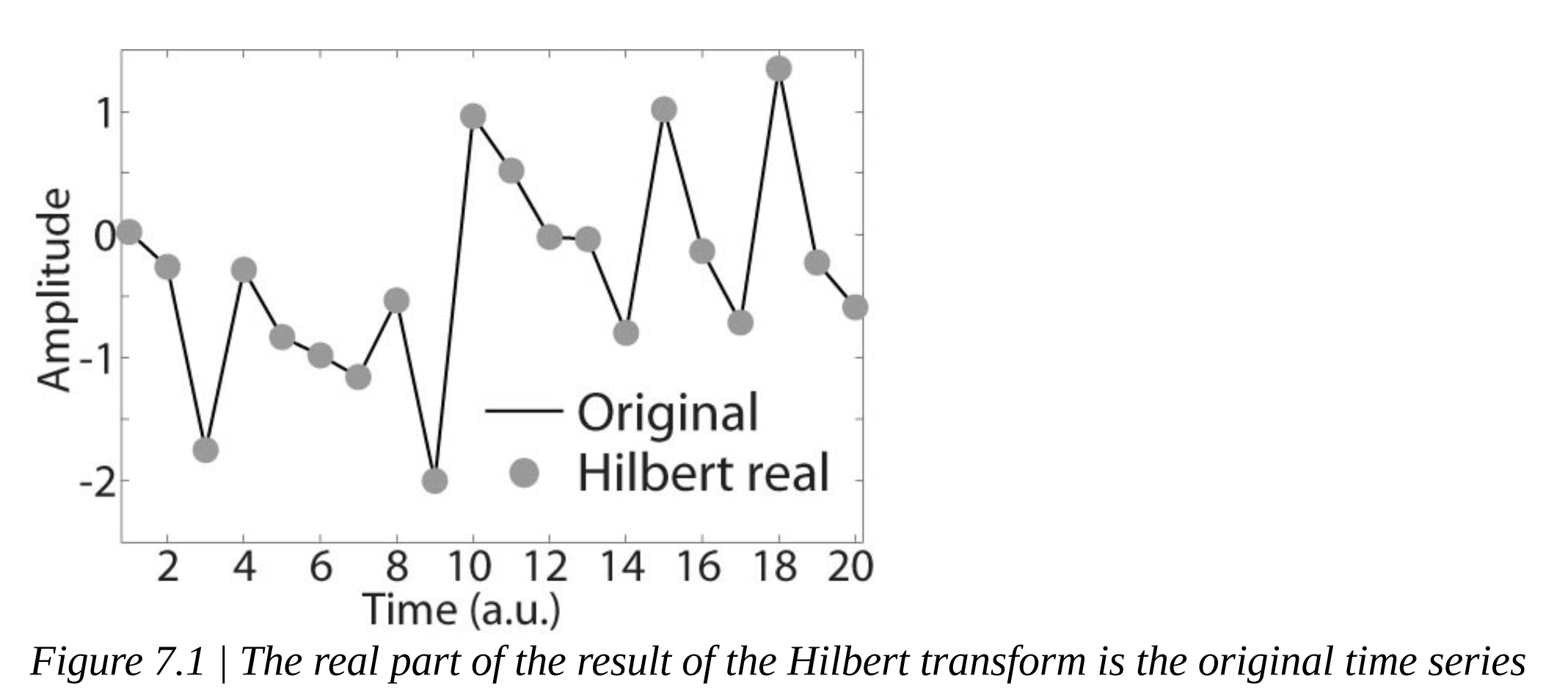
“The Matlab Signal Processing toolbox, and the Octave Signal package (free but not included with the typical Octave installation), contain a function called hilbert that will compute the Hilbert transform. You can also create your own function using the code above. The Hilbert transform does not affect the real part of a time series. This can be verified by plotting the real part of the Hilbert transform on top of the original time series.” (Mike X Fundamentals of Time-Frequency Analyses in Matlab/Octave, p. 96) Matlab信号处理工具箱和Octave Signal程序包(免费,但不包括typicall安装)包含一个希尔伯特函数来计算希尔伯特变换。也可以使用上面的代码创建自己的函数。希尔伯特变换不影响时间序列的实部。这可以通过在原始时间序列上绘制希尔伯特变换的实部来验证。

示例代码如下：

n=20; d=randn(n,1); dx=fft(d); 
posF = 2:floor(n/2); % positive frequencies 
negF = floor(n/2)+2:n; % negative frequencies 
dx(posF)=dx(posF)*2; 
dx(negF)=0; 
hilbertd = ifft(dx);
plot(d), hold on 
plot(real(hilbertd),'ro')